素性检验 - Miller-Rabin Test

由费马小定理可以知道，如果$p$是一个素数，且$(x, p)=1$，我们可以得到： $$ \begin{aligned} x^{p-1} \equiv 1 \pmod{p} \end{aligned} $$ 那么反之，如果有$x$满足$\forall a>1,(a,x)=1,s.t. a^x \equiv 1 \pmod{x}$，这样的$x$一定是素数吗？

很可惜的是，上述逆定理并不成立。

例如 561=3 * 17 * 11， $$\forall a>1,(a,561)=1, s.t.a^{560}\equiv1\pmod{561}$$

卡米歇尔数

• $n$是卡米歇尔数的充分必要条件是：
  • $n$无平方因子
  • $n$的每一个素因子$p$，有$p-1\mid n-1$
  • $n$是奇数且至少有三个不同的素因子

卡米歇尔数就是证伪上述逆定理的合数，即对任意$a>1,(a,n)=1$，都有$a^{n-1}\equiv1\pmod{n}$成立。

我们的目的是证伪，所以此处只证明充分性，至于必要性，读者自证不难。

设$n=\prod_{i=1}^{k}{p_i}$是一个米歇尔数，其中$p_i$是互不相同的奇素数。

对于任意$a>1,(a,n)=1$，则有$(a,p_i)=1$，由费马小定理知道 $$a^{p_i-1}\equiv 1 \pmod{p_i}$$

由于$p_i-1\mid n-1$，可以得到 $$a^{n-1}\equiv 1 \pmod{p_i}$$

所以$\forall a > 1, (a,n)=1$: $$a^{n-1}\equiv 1 \pmod{n}$$

虽然费马小定理的逆定理不成立，但人们发现，如果增加条件，可以得到类似的结果。

Miller Rabin Algorithm

由费马小定理可知，如果$p$是素数，$\forall a\in Z_p^*,a^{p-1}\equiv1\pmod{p}$

如果$p$为奇素数，那么我们可以得到$p-1$是一个偶数，则$p-1=k2^t,\textrm{k is odd}$

据此，我们再看看费马小定理： $$ \begin{aligned} \because \quad & a^{p-1}=a^{k2^t}\equiv1\pmod{p} \newline \therefore \quad & a^{k2^t}-1\equiv0\pmod{p} \newline \therefore \quad & (a^{k}-1)\prod_{i=0}^{t-1}{(a^{k2^i}+1)}\equiv0\pmod{p} \newline \end{aligned} $$

由此可知$p\mid(a^k-1)\prod_{i=0}^{t-1}{(a^{k2^i}+1)}$，即$p\mid (a^k-1)$或者$p\mid(a^{k2^i}+1),i=0,1,\dots,t-1$

Miller Rabin Algorithm 的算法流程的核心就是，检验这些因子之中是否有数能被$p$整除。

下面给出Miller Rabin Algorithm单次算法流程：

Given an odd integer $N$:

1. Pick $a$ random integer $a\in[1,N-1]$.
2. Write $N = 2^st + 1$, with $t$ odd, and compute $b = a^t \mod N$. If $b ≡ \pm1 \pmod{N}$, return true ($a$ is not a witness, $N$ could be prime).
3. For $i$ from $1$ to $s − 1$: a. Set $b \leftarrow b^2$ mod $N$. b. If $b \equiv −1 \pmod{N}$, return true ($a$ is not a witness, $N$ could be prime).
4. Return false ($a$ is a witness, $N$ is definitely not prime).

（这里的witness是指数a是该数为合数的一个凭证）

那么有可能出错吗？出错的可能性又是多少？

出错概率以及设置检验次数为多少比较合适

之前的推导中，我们似乎并没有看出该算法与直接判断$a^{n-1}\equiv1\pmod{n}$有何区别，似乎没有增加条件。

但其实，推导式在$n$是质数的情况给出的，合数情况下并不一定成立。

当$n$为合数时，$a^{n-1}\equiv1\pmod{n}$并不等价于$n\mid (a^k-1) \lor n\mid(a^{k2^i+1})$，但后者可以推出前者。

Miller-Rabin 甚至可以筛掉一些卡米歇尔数。

（应该挺显然的，但我当时看了很久……呜呜)

所以直接用费马小定理“逆”定理做素性检验的错误率会更大，一般不会选择。

接下来我们讨论单次素性检验出错的概率。

考虑一下同余方程$a\in Z_n^*, a^{n-1}\equiv1\pmod{n}$的解。若有解，则必然有$(a,n)=1$。

$\textrm{Proof:}$

如果该同余方程有解，则$\exists u,v\in Z,\textrm{ s.t. } va^{n-1}+un=1$

令$g=(a,n)$，则上式为$gN=1,N\in Z$

因此$(a, n)=g=1$.

如果$n$是奇合数，则在$Z_n^*$中导致单次Miller-Rabin Test通过的$a$应该属于这样一个集合：

$$S=\set{a:a\in Z_n^*,(a,n)=1,[n\mid(a^k-1)]\lor[n\mid(a^{k2^i}+1)]}$$

令$T=\set{a:a\in Z_n^*,(a,n)=1}$，易证明，$S < T$

由拉格朗日定理，$|S|\mid |T|$，即$|S|\mid\varphi(n)$；

又由于$|S|<|T|,\varphi(n)\leq(n-1)$，可知$|S|=\frac{\varphi(n)}{x}<\frac{n-1}{2}$

所以，概率为$P=\frac{|S|}{n-1}<\frac{1}{2}$。

下面给一个更加严格的证明¹，可以知道，这个概率小于$\frac{1}{4}$。

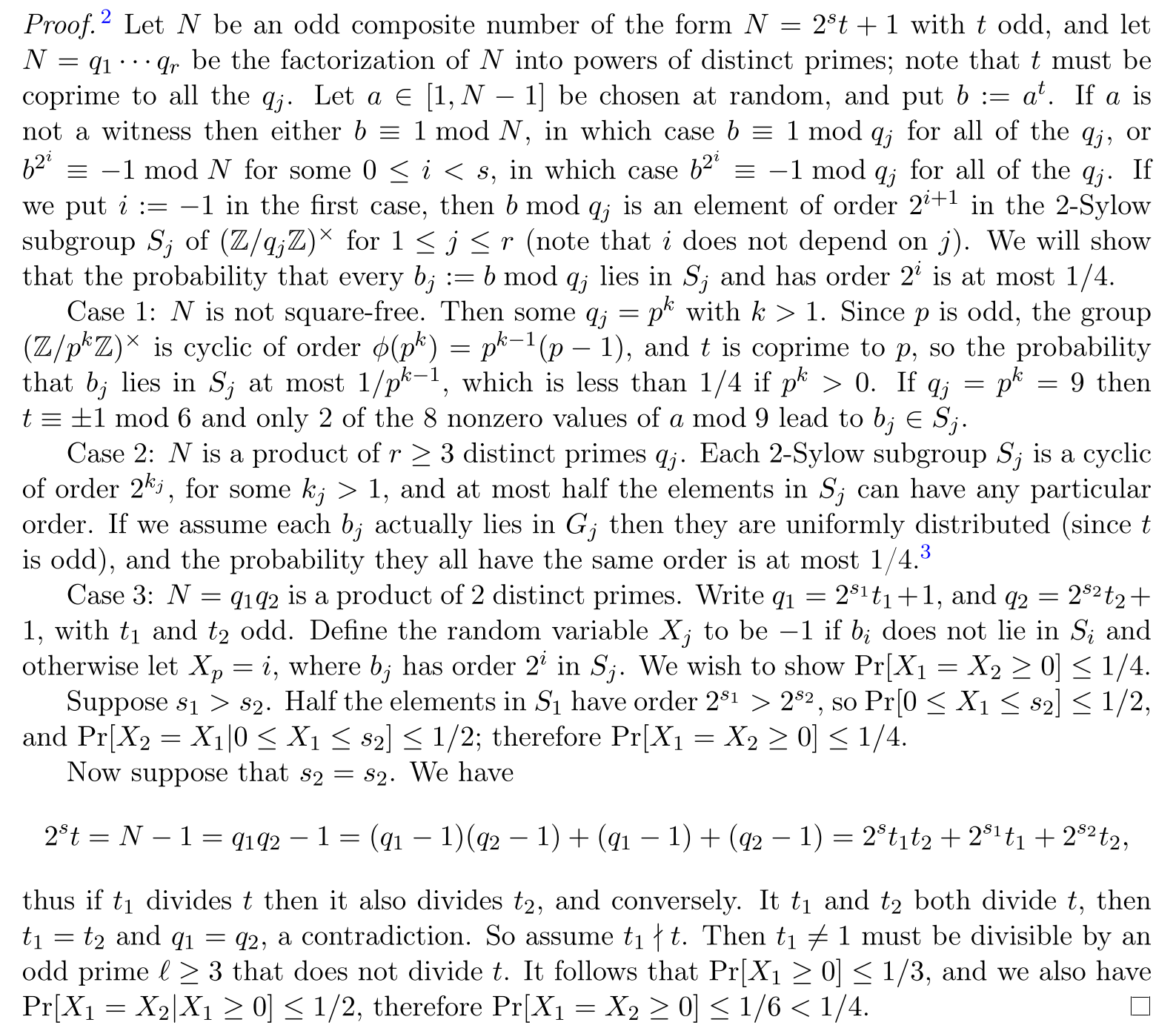
所以，这里设置为检验$10$次，检验结果为是素数的正确的概率大于$0.9999990463256836$，基本上不会出错了。

一个可以确保检验结果绝对正确的a集合

（INT_64，Jim Sinclair）²

1

2, 325, 9375, 28178, 450775, 9780504, 1795265022

Code

• 随机数写法的python3的代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

import random
import sys

def miller_rabin(n : int) -> bool:
    if n <= 1:
        return False
    if n == 2:
        return True
    k, t = n - 1, 0
    while not k & 1:
        k, t = k >> 1, t + 1
    if t == 0: # n是大于2的偶数
        return False
    for i in range(0, 10):
        a = random.randint(2, n - 1)
        tmp = pow(a, k, n)
        if tmp <= 1 or tmp == n - 1:
            continue
        for j in range(1, t + 1):
            if j == t: # 所有因子都不能被n整除
                return False
            tmp = tmp * tmp % n
            if tmp == n - 1:
                break
    return True

for num in sys.stdin:
    if miller_rabin(int(num)):
        print('Y')
    else:
        print('N')

• 使用SPRP的python3代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

import sys

def miller_rabin(n : int) -> bool:
    if n < 2 or n % 2 == 0: return n == 2
    k, t = n - 1, 0
    while ~k & 1:
        k, t = k >> 1, t + 1
    for a in {2, 325, 9375, 28178, 450775, 9780504, 1795265022}:
        tmp = pow(a, k, n)
        if tmp <= 1 or tmp == n - 1: continue
        for j in range(0, t + 1):
            if j == t: return False
            tmp = pow(tmp, 2, n)
            if tmp == n - 1: break;
    return True

for num in sys.stdin:
    if miller_rabin(int(num)):
        print('Y')
    else:
        print('N')

• 但是python3的效率实在太慢，不能在算法竞赛中使用，下面给出c++的代码作为模板。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

using ull = unsigned long long;
ull modmul(ull a, ull b, ull M) {
  ll ret = a * b - M * ull(1.L / M * a * b);
  return ret + M * (ret < 0) - M * (ret >= (ll)M);
}
ull modpow(ull b, ull e, ull mod) {
  ull ans = 1;
  for (; e; b = modmul(b, b, mod), e /= 2)
    if (e & 1) ans = modmul(ans, b, mod);
  return ans;
}
bool miller_rabin(ull n) {
  static const vector<ull> SPRP = {
    2, 325, 9375, 28178, 450775, 9780504, 1795265022
  };
  if (n == 1 || n % 6 % 4 != 1) return (n | 1) == 3;
  ll t = __builtin_ctzll(n - 1), k = (n - 1) >> t;
  for (const ull &a : SPRP) {
    ull tmp = modpow(a, k, n);
    if (tmp <= 1 || tmp == n - 1) continue;
    for (int i = 0; i <= t; i++) {
      if (i == t) return false;
      tmp = modmul(tmp, tmp, n);
      if (tmp == n - 1) break;
    }
  }
  return true;
}

参考来源