Cpp Tricks - 语言向进阶（？）指南

尽量只使用宏：

1
2
3

using i64 = long long;
#define all(a) begin(a), end(a)
#define sz(x) (int)((x).size())

参考

• cppreference 中文参考手册

常见容器

• string
• array - vector - deque
• map - multimap - unordered_map
• set - multiset - unordered_set
• stack - queue - prority_queue
• pair - tuple
• bitset

支持顺序访问（或迭代器使用std::next，std::prev顺序访问）的容器可以用下面的办法快速枚举：

1
2
3
4

for (auto value : container) {
  // value 为容器中的元素
  // auto  为c++11加入的，可以自动推断元素类型
}

对于结构体，一定程度上可以使用tuple代替。

1
2
3

tuple<type_1, type_2, ....> container;
// 或者 struct，按照定义变量的顺序来即可
for (auto [value_1, value_2, ...] : container) {...}

1
2
3
4

tuple<int, int> container;
int a, b;

tie(a, b) = container;

关于Range-based for loop的一些问题

• 使用for (auto val : v)确实会发生拷贝，但并不是说v中元素就一定不会改变

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

#include <bits/stdc++.h>
using namespace std;

int main() {
  int n = 5;
  vector<bool> v(n, true);
  for (auto val : v) val = false;
  for (int i = 0; i < n; i++) {
    cout << (v[i] ? "true" : "false");
    cout << " \n"[i + 1 == n];
  }
  return 0;
}

/** output: 
false false false false false
**/

不过，会出现上面情况的应该也就是vector<bool>这个奇葩了。显然auto判断类型为_Bit_reference，通过下面代码可以验证：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

#include <bits/stdc++.h>
using namespace std;

int main() {
  cout << boolalpha;
  vector<bool> v = {false};
  for (auto val : v) {
    cout << is_same<_Bit_reference, decltype(val)>::value << '\n';
  }
  return 0;
}

/** output: 
true
**/

同时，如果你使用了auto &val : v，那么你将面临下面的报错：

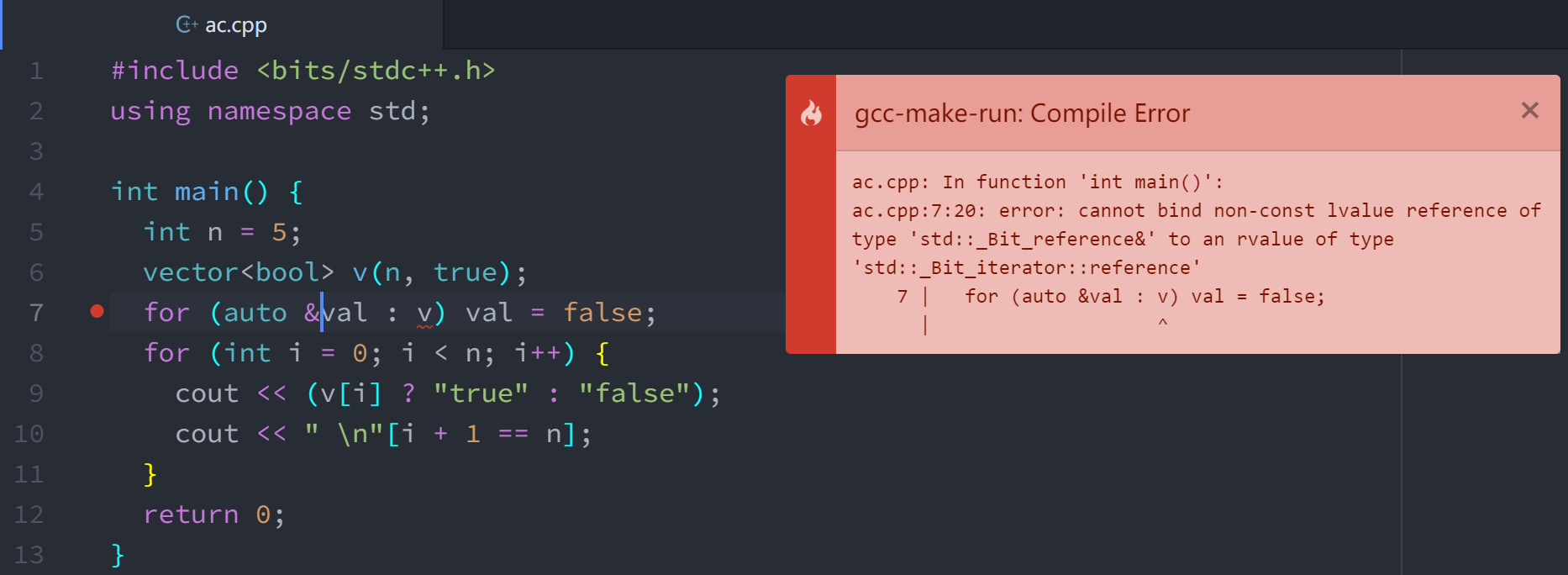
• 如果想用auto自动识别变量类型的引用，但又不想出错，你应当使用auto &&val : v来代替。
• 使用const auto &val : v来彻底避免内存拷贝以及保证元素不被修改。

迭代器 与 all()宏

1

#define all(a) begin(a), end(a)

在c++的STL中，更常用的是迭代器，而非下标（指针），这与纯C写法有较大区别。

• begin()，end() 作为容器的起始迭代器和末尾的迭代器。
• rbegin()，rend() 逆向的迭代器。

1
2

sort(a.begin(), a.end());
sort(begin(a), end(a)); // C++11 已支持

1
2

sort(a.rbegin(), a.rend());
sort(rbegin(a), rend(a)); // C++14 已支持

用于遍历的函数如下（虽然有许多容器的迭代器重载了++和--，可以直接像下标一样处理，但还是推荐）：

1
2

prev(iterator) // 上一个迭代器
next(iterator) // 下一个迭代器

定义这个宏的原因是：使用算法库的函数经常需要填写迭代器范围。

1
2

std::vector<int> a {...};
std::ranges::sort(a); // 而不是 sort(a.begin(), a.end());

算法库

此处仅记录一些本人常用的部分，事实上<algorithm>内容十分丰富，并且还在随版本更新。Cpp对于并行优化的支持也逐渐完善，出现了<ranges>这种十分方便的库。一些类似MATLAB的矢量化结构也有望加入到C++26的标准之中，感兴趣的可以观看CppCon 2023的一个分享：std::linalg: Linear Algebra Coming to Standard C++ - Mark Hoemmen。

惟愿本文能抛砖引玉，引起读者的兴趣。参阅 cppreference - algorithm。

排序 std::sort

std::sort()，应该是一个很常见的函数，用来排序数组的时，一些偏向C的写法会使用头尾指针来确定范围，再写外部函数确定排序规则。

但是，在使用如vector等可以排序的容器时，我们一般会动态开空间，所以此时待排序的范围就是全部元素。(或者对起始和终止的迭代器进行运算，以获得合适的排序范围)

1
2
3
4
5
6

vector<int> a(n);
sort(all(a)); // 对全部元素排序
sort(1 + all(a)); // 对下标从 1 开始的部分排序

sort(all(a), less<int>()); // 升序 （默认）
sort(all(a), greater<int>()); // 降序

与std::sort比较相似的还有std::stable_sort，后者是能够保证，相同大小的元素在排序前后的相对位置不变。

• 检验数组是否有序：std::is_sorted()

关于 lambda 表达式 (c++11)

在sort函数中，第三个参数可以为我们定义的排序规则，如果不使用lambda表达式，我们往往会把它们写在外面，然后填写函数指针。

基础语法如下：

1
2
3
4
5
6

[ captures ] ( params ) specs requires(optional) { body }

[ 获取的变量 &表示引用，=表示传值 可以写多个变量，但一般缺省，只写& ]
( 在表达式中定义的变量 )
specs requires(optional) 一般缺省，或者写成 -> 返回值类型，如 -> int
{ 具体表达式 函数体 }

放在sort中使用的实例：

1
2
3
4
5
6
7
8
9

struct Node {
  int a, b;
  Node(int _a = 0, int _b = 0)
    : a(_a), b(_b) {}
};

sort(all(v), [&](const Node &p, const Node &q) {
  return p.a * q.b <= q.a * p.b;
});

更多的，如果关联使用<functional>，可以将外部函数写在主函数内。

• 这里还有一个问题，那就是如何写递归函数？

使用 function 类是一种解决办法，如下面的dfs代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

constexpr int V = 100;
vector G(V, vector<int>(V));

function<void (int, int)> dfs = [&](int u, int fa) {
  for (auto v : G[u]) {
    if (v == fa) continue;
    dfs(v, u);
  }
};
dfs(source, -1); // 使用方式

如果不按照function类来声明该函数，[ captures ]无法获知自己的存在，所以一个可行的方案就是，在传值的时候将自己传入。

1
2
3
4
5
6
7

auto dfs = [&](auto self, int u, int fa) {
  for (auto v : G[u]) {
    if (v == fa) continue;
    self(self, v, u);
  }
};
dfs(dfs, source, -1); // 注意调用时需要将 自己 传入

按照某些人的说法，使用第二种方式（也就是将“自己”传入）会有更好的性能，理由是更容易获得内联优化。笔者对此持怀疑态度，但也并未验证，仅凭个人经验，这两种方式至少不会出现较大的性能方面的差异。如有读者验证过，不妨在评论中或者以其它方式告知。

搜索相关

我们知道，对于有序容器，我们可以利用其单调性来进行二分。

• 进行了上面的排序操作，我们的数组（暂且这么称呼）已经变得有序，如何利用STL中写好的二分函数呢？

对于一般容器而言，二分函数的写法比较统一（以vector<int> a为例好了）：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

vector<int> a { 0, 1, 2, 2, 2, 3, 4 };

// 第一个大于等于 value 的位置（迭代器）
auto it = lower_bound(all(a), value); 

// 第一个大于 value 的位置（迭代器）
auto it = upper_bound(all(a), value); 

// 同时获得上述两者 返回为 std::pair<ForwardIt, ForwardIt>
auto P = equal_range(all(a), value);

1
2

set<int> S;
auto it = S.lower_bound(value);

更一般的情况是，我们只需要数组中最值。

1
2
3
4

auto it_min = min_element(all(v)); // 最小元素对应的迭代器（可以理解为下标）
auto it_max = max_element(all(v)); // 最大元素

cout << *it_min; // 用于输出

• 如果你需要知道是一个数组的第$K$大的数（比如中位数），该怎么办呢，直接排序吗？

在某些时候，我们可能连$\mathcal{O}(n\log n)$的算法也无法接受， 此时可以使用均摊复杂度为$\mathcal{O}(n)$的函数nth_element()

1
2
3
4
5
6

vector<int> a {4, 5, 3, 1, 6, 2};
int k = 2;
nth_element(a.begin(), next(a.begin(), k), a.end());
for (int x : a) cout << x << ' ';

// 输出：2 1 3 4 5 6  ...  a[k] = 3

可以见，该函数并非排序，而是将前$K$小的数放在最前面的$K$个位置，且令第$K+1$位上为第$K+1$大。（原理上nth_element()可以使用快速排序的思想完成。实际使用中，需要注意范围左闭右开）

如果仅仅需要一般的查找，使用find或者find_if即可，后者搭配lambda表达式，可以按需搜索。使用时请注意复杂度，对于一般容器，该函数使用的是顺序遍历，时间复杂度为$\mathcal{O}(n)$。若find()查找元素无果，返回的迭代器为end()。特别的，string中find失败得到的是string::npos。

计算相关

• count 和 count_if。

统计元素个数时可用前者 count(all(a), val) ，如果需要按满足条件来统计，使用后者再搭配上lambda表达式即可。值得说明的一点是，map和set中的find和count函数的复杂度是$\mathcal{O}(\log n)$，可以放心使用。

• all_of any_of none_of。

顾名思义，对于一个范围，判断满足条件（一般用lambda表达式写）的集合与全集的关系。

• partial_sum。

前缀和函数，partial_sum(all(a), begin(b))，此处的 b 需要先开够空间。类似的还有前向差分函数。

• accumulate

比较常见的要求是对数组求和，我们直接利用accumulate(all(a), 0)即可，但是该函数还有许多值得探究的部分（cppreference - accumulate）。

注意，在accumulate参数中，求和并非恒定不变，使用lambda表达式或者重载符号+也能够对其修改。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

struct str_node {
  str s; // define str string
  str_node operator +(const str_node &oth) const {
    return str_node{this->s + " + " + oth.s};
  }
};

void example() {
  vector<str_node> a{ 
                      str_node{"abc"},
                      str_node{"123"},
                      str_node{"def"},
                      str_node{"456"},
                      str_node{"!@#"}
                   };
  str_node sum = accumulate(1 + all(a), a.front());
  cout << sum.s << endl;
}

// 输出：abc + 123 + def + 456 + !@#

1
2
3
4
5
6
7
8
9

template<class InputIt, class T>
constexpr // since C++20
T accumulate(InputIt first, InputIt last, T init)
{
    for (; first != last; ++first) {
        init = std::move(init) + *first; // std::move since C++20
    }
    return init;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

template<class InputIt, class T, class BinaryOperation>
constexpr // since C++20
T accumulate(InputIt first, InputIt last, T init, 
             BinaryOperation op)
{
    for (; first != last; ++first) {
        init = op(std::move(init), *first); // std::move since C++20
    }
    return init;
}

1
2
3
4
5
6
7
8

vector<long long> v;
...
long long sum = accumulate(all(v), 0);

// 正确的写法如下：
// long long sum = accumulate(all(v), 0LL);
// 或者
// long long sum = accumulate(1 + all(v), v.front());

Bit相关

这部分主要和c++20标准库头文件<bit>相关，但是考虑到现在许多的编译器还未能完全支持c++20，因此在后面加入了一部分来自GCC Built-in Functions的位操作函数。

c++20 <bit>常用的函数

• has_single_bit 检查一个数是否为二的整数次幂
• bit_ceil 寻找不小于给定值的最小的二的整数次幂
• bit_floor 寻找不大于给定值的最大的二的整数次幂
• countl_zero 从最高位起计量连续的 0 位的数量
• countl_one 从最高位起计量连续的 1 位的数量
• countr_zero 从最低位起计量连续的 0 位的数量
• countr_one 从最低位起计量连续的 1 位的数量
• popcount 计量无符号整数中为 1 的位的数量

bitset 容器

补充一个不怎么常用的容器，bitset本质上就是一个01序列。

其占用内存很小并且也重载了位操作（&, |, >>, <<等）因此有时也用于卡常数。

常用的操作大致如下（以bitset<N> b;为例）：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

b.all();
b.any();
b.none();
// 检查是否所有、任一或无位被设为 true

b.count();  // 返回设置为true的位的数量
b.set();    // 将位置为 true
b.reset();  // 将位置为 false
b.flip();   // 翻转位的值

b.to_ullong();
// 转换 bitset 的内容为 unsigned long long 整数
// bitset 的首位对应数的最低位，而尾位对应最高位
// 若值不能以 unsigned long long 表示，则为 std::overflow_error

来自GCC Built-in Functions的位操作函数

官方的介绍 https://gcc.gnu.org/onlinedocs/gcc/Other-Builtins.html

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

__builtin_clz()        // count leading  0s   前面0的数目
__builtin_ctz()        // count trailing 0s   后面0的数目
__builtin_popcount()   // count bit 1         比特位为1的数目

/**
(16)10 = (00000000 00000000 00000000 00010000)2
__builtin_clz      : 27
__builtin_ctz      :  4
__builtin_popcount :  1

对于 long 类型的在函数名后面加 'l'
对于 long long 类型的在后面加 'll' 如 __builtin_popcountll
*/

既然写到了gcc的内建函数，不妨也提一下其它的双下划线函数：

• __gcd()，顾名思义，一个用于求两数最大公因数的函数。

值得注意的是，在c++17中，已经加入了gcd()函数，可以不加下划线使用。

• __builtin_ia32_rdtsc()

rdtsc的原文大概是Read Time Stamp Counter，这个函数原本是用于测量cpu时钟的，用于竞赛大概只能生成随机数种子。所以为什么在这提呢？主要是由于我的随机数生成代码中包含这一个函数。

1
2
3
4
5
6
7
8
9

#include <random>

std::mt19937 rng(__builtin_ia32_rdtsc());
template<typename T> inline T randint(T l, T r) {
  return std::uniform_int_distribution<T>(l, r)(rng);
}
template<typename E> inline E randreal(E l, E r) {
  return std::uniform_real_distribution<E>(l, r)(rng);
}

位运算的其它操作

• ^ 异或

对于二值集合{a, b}，如何找到不同与x的另一个数呢？，直接if-else判断当然可以，但没必要。最快的写法利用相同数的异或为0，同时任何数与0异或都等于它本身这两个所有人熟知的性质，写成x ^ a ^ b就可以了。

• 二进制枚举

主要是在dfs由数组确定的集合时用到，当然直接写dfs也是可行的，甚至更快。（但，私以为二进制枚举最优雅）

• 取模$2^k$

等价为 & 上 $2^k-1$。用法大概是，最后 & 一下就行（大概。

注意，$2^{32}-1$需要int64_t。此时用uint32_t自然可以，但是会比有符号的慢。

• lowbit, submask enumeration 等需要在具体的数据结构和算法中使用的技巧，这里就不展开介绍了，可参考如下链接或者自行去OI-Wiki查询。
  • 树状数组 - Fenwick Tree
  • 子集DP - SoSDP

更多信息可参阅 Bit manipulation - Algorithms for Competitive Programming

I/O相关

I/O在竞赛中的影响其实不算大，虽说某些“歪门邪道”对于卡常数十分执着，但这毕竟不是竞赛所考核的重点。 但是，由于语言特性的关系，某些“语言小白”的代码可能因此从AC变成TLE，这也是本部分独立出来的目的。

同步流

同步流是cpp关于c的兼容性处理。从字面意思上理解，“同步”和“流”就是这一机制的关键。

• cpp的流：std::cin、std::cout、std::cerr、std::clog 以及“宽字符流”的std::wcin、…、std::wclog
• c的流：stdin stdout stderr

同步流就是让C++流与标准C流在每次输入/输出操作后同步。

1
2

std::ios_base::sync_with_stdio(false);
std::cin.tie(nullptr);

不介意警告信息（也不会由编译器报啦，只是写法不太规范的问题）可以写成一行

1

cin.tie(nullptr)->sync_with_stdio(false);

1

std::cout.tie(nullptr);

• 关闭了同步流，意味着scanf/printf, cin/cout等不再同步，C++流拥有自己的同步独立的缓冲区。
  • 这使得混合C和C++风格的I/O非常危险，所以最好不要混用！！！
• std::endl会导致flush，请使用\n换行（事实上理应如此，工程中也建议这样做）。
  • cin.tie(nullptr); + cout << endl; 等于白忙活一场且TLE
• std::setprecision() 等也会导致flush，只要设置一次就好了。
• 对于交互题，IO性能完全不用考虑，请不要写cin.tie(nullptr)。

关闭同步流不是 FAST IO

如上文所述，关闭同步流只是恢复正常，不算快读！真正的快读，你应该自己实现BufferedReader + fread/fwrite

• 如果你是在要，那我只能……偷大佬的板子 Nyaan’s Library - misc/fastio.hpp

浮点数、O2 和 Windows (O.o?)

在 codeforces 你可能会遇到（但是其它使用 Linux 环境评测的不会），浮点数读入和O2负优化。 (2024-01-20 实测Bug无法复现了，悲~) 就当记录历史吧。

• Why std::cin has such a low efficiency when processing float points on Codeforces?
• read doubles faster in cpp

目前，只要不选择 GNU G++17 7.3.0 非64位 的提交选项就不会触发此问题。

1
2
3
4
5
6
7
8
9

friend auto operator>>(std::istream& is, Point& _p) -> std::istream& {
-  return is >> _p.x >> _p.y;
+  static std::string s;
+  std::cin >> s;
+  _p.x = std::stod(s);
+  std::cin >> s;
+  _p.y = std::stod(s);
+  return is;
}

在某些有点历史的代码，你可能会看见类似上面这种操作（std::stod()是string -> double的转换函数）。 不要喷他们代码得烂，他们只是遇到了bug（

IO写法技巧

• cin.exceptions() 如果看我的代码的话，你会发现下面这行：

1

std::cin.exceptions(std::istream::failbit);

这是为了捕获读入（类型）错误，其用处是：codeforces交错问题，让它在第一个样例RE（如果读入方式完全一样就认命吧），从而不增加罚时。

注意，这和 while(cin >> ...) 或者 while(scanf(...) != EOF) 的多组输入模式有冲突。原因似乎是，while的终止条件就是 istream::failbit 置位（然后被捕获，触发RE）。

• cout << " \n"[i == n]; 避免行末空格，原理见我的另一篇博客。
• 文件I/O，怎么用C++的风格？
  • 其实没必要，用freopen + scanf/printf吧
  • 非要用，使用ifstream/ofstream吧
    • 什么？你还要cin/cout?
    • 那就把cin.rdbuf()重定向吧。

如下是一个完整的例子

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

  std::ios_base::sync_with_stdio(false);
  std::cin.exceptions(std::istream::failbit);
  std::cin.tie(nullptr);
// 在编译指令里加 -DKENSHIN ，只在本地使用文件输入输出
#if defined(KENSHIN)
  std::ifstream input("_.in");
  std::ofstream output("_.out");

  std::cin.rdbuf(input.rdbuf());
  std::cout.rdbuf(output.rdbuf());
#endif

  std::cout << std::fixed << std::setprecision(15);

杂项 与 写法上的技巧

• iota(all(a), val)

从val开始递增地赋值，赋值后地数组为 { val, val + 1, ... }。

十分适合用来写并查集的初始化（当然，还有不同的写法是初始化成-1）。

• auto [min_val, max_val] = minmax(a, b)

同时获得两数的最大值和最小值，啥用没用 实际使用很少。

低版本建议的写法是 tie(min_val, max_val) = minmax(a, b) ，需要先声明变量。

1
2
3
4

tie(a, b) = minmax(a, b)

   a = (const T&) b
   b = (const T&) a // 此时，由于此处为 a 的引用，所以值已经改变

• rotate 旋转，放在圆（环）上理解可能会好点。

1
2
3
4
5

template< class ForwardIt >
void rotate( ForwardIt first, ForwardIt n_first, ForwardIt last );

rotate(a.begin(), next(a.begin(), 2), a.end()); 
// a.begin() + 2, a.end() 和 a.begin(), a.begin() + 2 整体交换位置

• 求数组中不同元素的个数

1

int num = sz(set<int>(all(a)));

• next_permutation 和 prev_permutation

枚举数组的所有排列，常见的写法是：

1
2
3
4

sort(all(p));
do {
  // ... 
} while (next_permutation(all(p)));

• substr

string中的STL用得比较少，一般使用的就是substr获取子串。

1

s.substr(start，length); // length 参数缺省时表示后续直到 end()

• std::vector 内存回收问题。举个例子CF1706D2。

对于std::vector而言，pop_back()，clear()，resize()都不会立即回收已经使用过的内存（程序做的应该只是迭代器的移动操作，具体细节本人未作研究，建议读者自行查阅STL的相关源代码）。这大抵是为了方便后续的写入，省去再次分配空间的消耗。要做到立马回收空间，行之有效的方式是，利用std::swap()的机制，将使用的内存交换走。

1

vector<T>().swap(v);